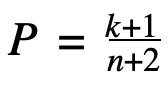The Sunrise Problem and Investing
Applying Laplace's Rule of Succession to Investments
“What is the probability that the sun will rise tomorrow?”
This is the Sunrise Question by the French scholar Pierre-Simon Laplace.
He treated this problem by using the Rule of Succession. This is how it is written in Wikipedia
In the Wikipedia example, if we saw the sunrise 10,000 times, the probability that the sun rises tomorrow = 10001 / 10002 ≈ 0.99990002, or 99.990002%.
The rule of succession is a bit more useful other than just calculating the probability of the sun rising tomorrow. The more famous application used in textbooks is pulling black and white marbles from a url.
If you draw black marbles 8 times (k) out of 10 (n), what is the probability that the next draw will be a black marble?
The formula is
The probability that the next marble will be black given that you drawn 8 marbles out of 10 is (8+1) / (10+2) = 75%, according to the law of succession.
The above formula, if applied to the sunrise problem, will be that there were 10,000 sunrises out of 10,000 days, so the k and n are both 10,000.
I use this formula to check the investment returns of a fund using its past performance. It is not a precise calculation, but easy enough for me to get a sense of the fund.
For example, I have a fact sheet of a hedge fund that was launched in 2013. The fact sheet has 8 calendar year returns of which 7 was positive. The probability of this fund with have another positive year in 2021 is 80% (and as of May, it is up 11.85%, looking good).*
Since it is a hedge fund and I expect them to do better than just positive returns, I can use the formula to calculate the possibility of returns higher than 5%. It turns out that 6 out of 8 years the fund had a 5%+ return, so the probability that the fund will have a higher than 5% return this year is 70%.
This is not a fancy way to analyse a fund or strategy. The volatility, Sharpe ratio, Sortino ratio, maximum drawdown, months to recover, correlation… are all in this fact sheet and all important figures. All useful to those who are in the analysis business. All important if you are managing your assets against liabilities. But for someone looking for an above inflation rate return (i.e., me), those are not the most important information**.
80% or 70% is, obviously, not 100%. There is a chance that the fund will generate negative returns or only end with lower than 5% return in 2021. As they say, “Past performance is not indicative of future returns.” You cannot rely just on past performance to make an investment decision.
What I like about this calculation method*** is that no matter how large the sample, the probability would never be 100%. Even for the sunrise example above with 10,000 observations, there is a tiny chance that the sun will not rise tomorrow (a supernova event?).
And that is a good reminder for me that there is nothing in investment that is 100%.
* Assuming the fund continues to do well in 2021 and ends as another positive year, the probability that this fund will have a positive return in 2022 would be 81.8% ((8+1)/(9+2)=81.8%). On the other hand, if the latter half of this year turns to be difficult for this fund and it ends in negative territory, the probability that this fund will have a positive return in 2022 will be 72.7%, still not bad. This methodology allows you to add new information to re-calculate the probability.
** I use the monthly returns provided in the fund fact sheet and calculate rolling returns. I intend to cover that in a future post.
*** It allows you to calculate the probability with small sample sizes; that is also useful.